Introduction to Bayesian Analysis

CMOR Lunch’n’Learn

11 April 2024

Ross Wilson

What is the objective of a statistical analysis?

  • Consider, for example, a clinical trial to estimate a treatment effect

  • We may want to know:

    • What is the ‘true’ (average) treatment effect?

    • How certain are we about that estimate?

      • What is the range of plausible values of the effect?

      • What is the probability that the treatment is ‘effective’?

Classical versus Bayesian approaches

Classical versus Bayesian approaches


  • We’ll try not to go into too much technical detail


  • A useful way I have seen it described:

    • Classical methods tell us what the observed data (e.g. from this trial) tell us about the treatment effect

    • Bayesian methods tell us how we should update our beliefs about the treatment effect based on these data

Brief review of classical statistics

  • Maximum likelihood - what true value of the treatment effect is most compatible with observed data?

    • For what value of the treatment effect are the observed data most likely to occur?

  • Hypothesis testing - how likely is it that the observed data could be due to chance alone?

    • If there is no true effect of treatment, how likely would the observed (or larger) effect be?

  • Confidence intervals - what range of values can we be ‘confident’ the treatment effect falls within?

    • Almost, but not quite: There is a (say) 95% probability that the true effect lies within the 95% confidence interval

What is Bayesian analysis?


  • A probabilistic approach to data analysis and interpretation


  • Conceptually, we consider the treatment effect to be a random variable

    • We can express our beliefs about the value of this variable as a probability distribution


  • How should we refine our prior beliefs in light of new data?

Conditional probability


  • Probability is conditional on available information

  • What is the probability it will rain in Dunedin tomorrow?

    • \(\mathrm{Pr}(\text{Rain tomorrow})\)

    • \(\mathrm{Pr}(\text{Rain tomorrow}\ |\ \text{Today's weather})\)

    • \(\mathrm{Pr}(\text{Rain tomorrow}\ |\ \text{Tomorrow's forecast})\)


  • Even the first (unconditional) probability is implicitly conditional on some information set (e.g. your general knowledge about Dunedin’s rainfall patterns)

What is Bayesian analysis?


  • Bayesian analysis is the process of updating these probabilities in light of new information
  • That is, given new \(\mathit{data}\), how should we get from

\[\mathrm{Pr}(A)\]

to

\[\mathrm{Pr}(A\ |\ \mathit{data})\]


Bayes’ Theorem:


\[\mathrm{Pr}(A | B) = \frac{\mathrm{Pr}(B | A) \mathrm{Pr}(A)}{\mathrm{Pr}(B)}\]


  • In a statistical model, we are usually interested in probability distributions over continuous variables:

\[f(\theta | y) = \frac{f(y | \theta) f(\theta)}{f(y)}\]

(updated knowledge about a parameter \(\theta\) given data \(y\))

Bayes’ Theorem


  • Tells us how to calculate the ‘posterior distribution’ given:
    • an assumed data generating model
    • prior information/beliefs about the parameter(s)
    • current data

\[f(\theta | y) = \frac{f(y | \theta) f(\theta)}{f(y)}\]

\[\mathrm{Posterior} \propto \mathrm{Likelihood} \times \mathrm{Prior}\]

  • Informally: updated belief = current evidence \(\times\) prior evidence or belief

Bayes’ Theorem

  • In principle:

    • we start with some beliefs about the parameters of interest

    • review those beliefs in light of the evidence at hand

    • and calculate an updated belief as a combination of the prior and the new evidence

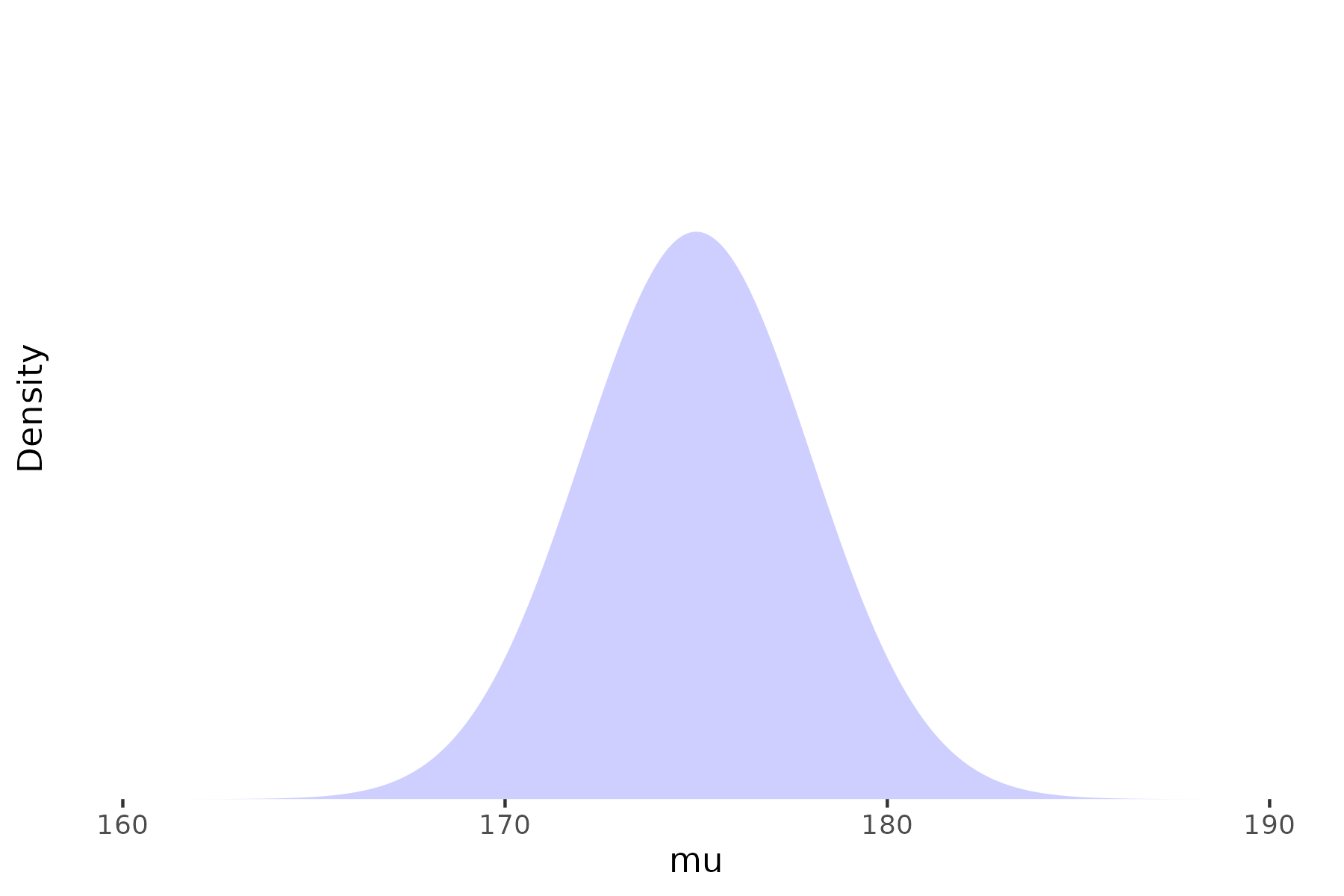
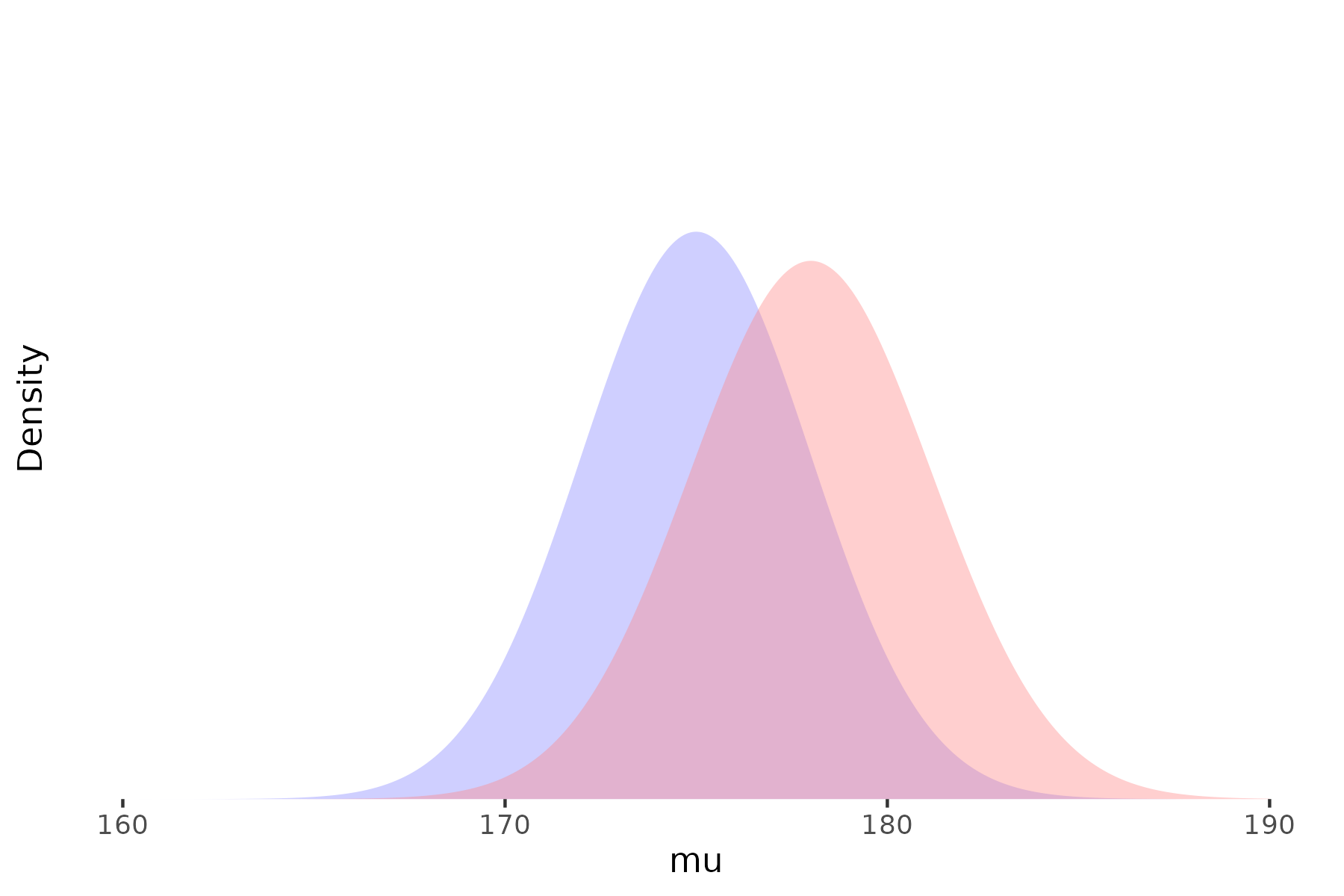
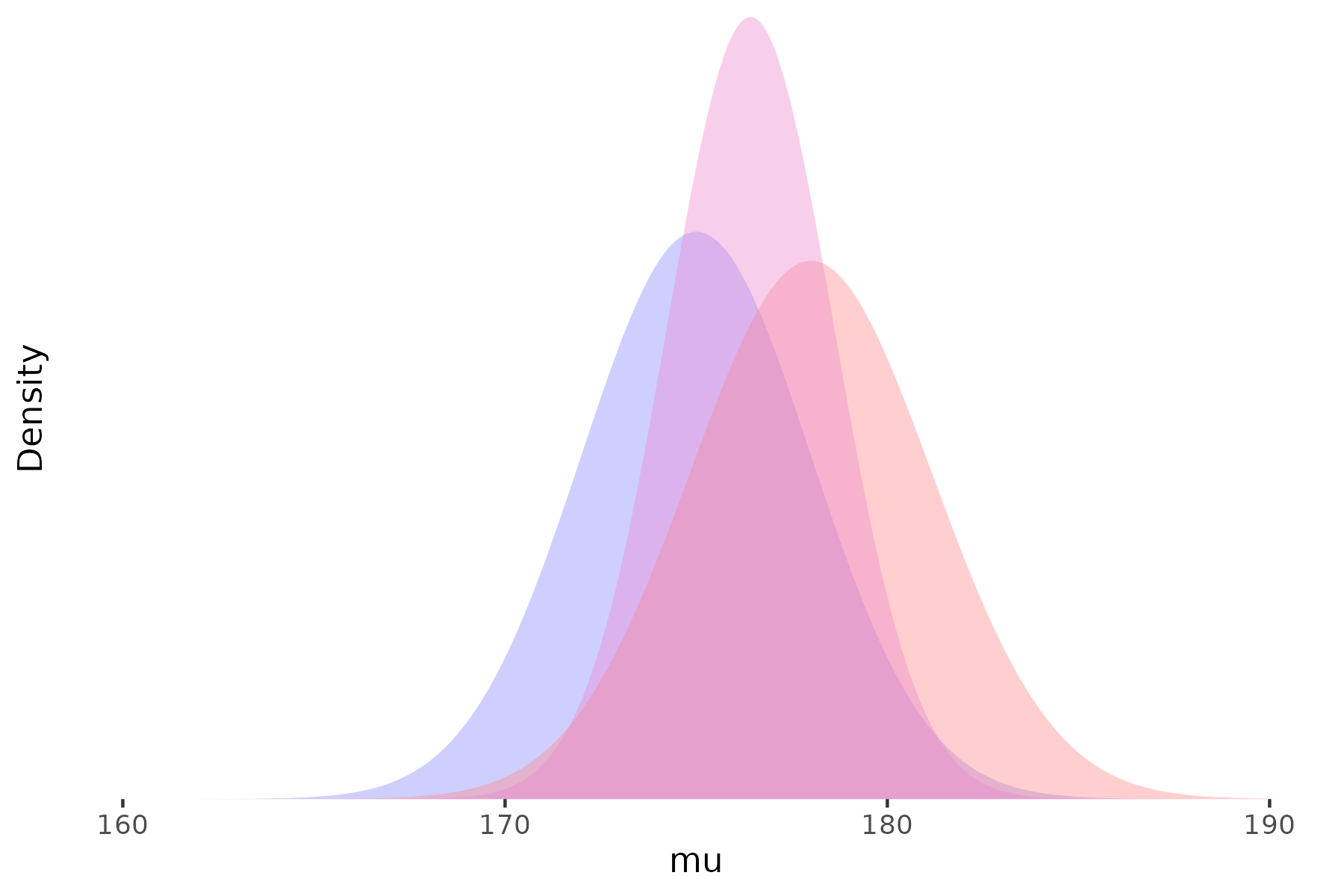
Prior

Likelihood

Posterior

Specifying priors

  • The role of prior beliefs has been the most controversial aspect of Bayesian analysis

  • Where do our ‘priors’ come from?

    • Previous research

    • Common sense/intuition?

    • ‘Weakly informative’ or ‘non-informative’ priors

  • In most cases there is no ‘correct’ prior, and sensitivity to various plausible priors should be considered
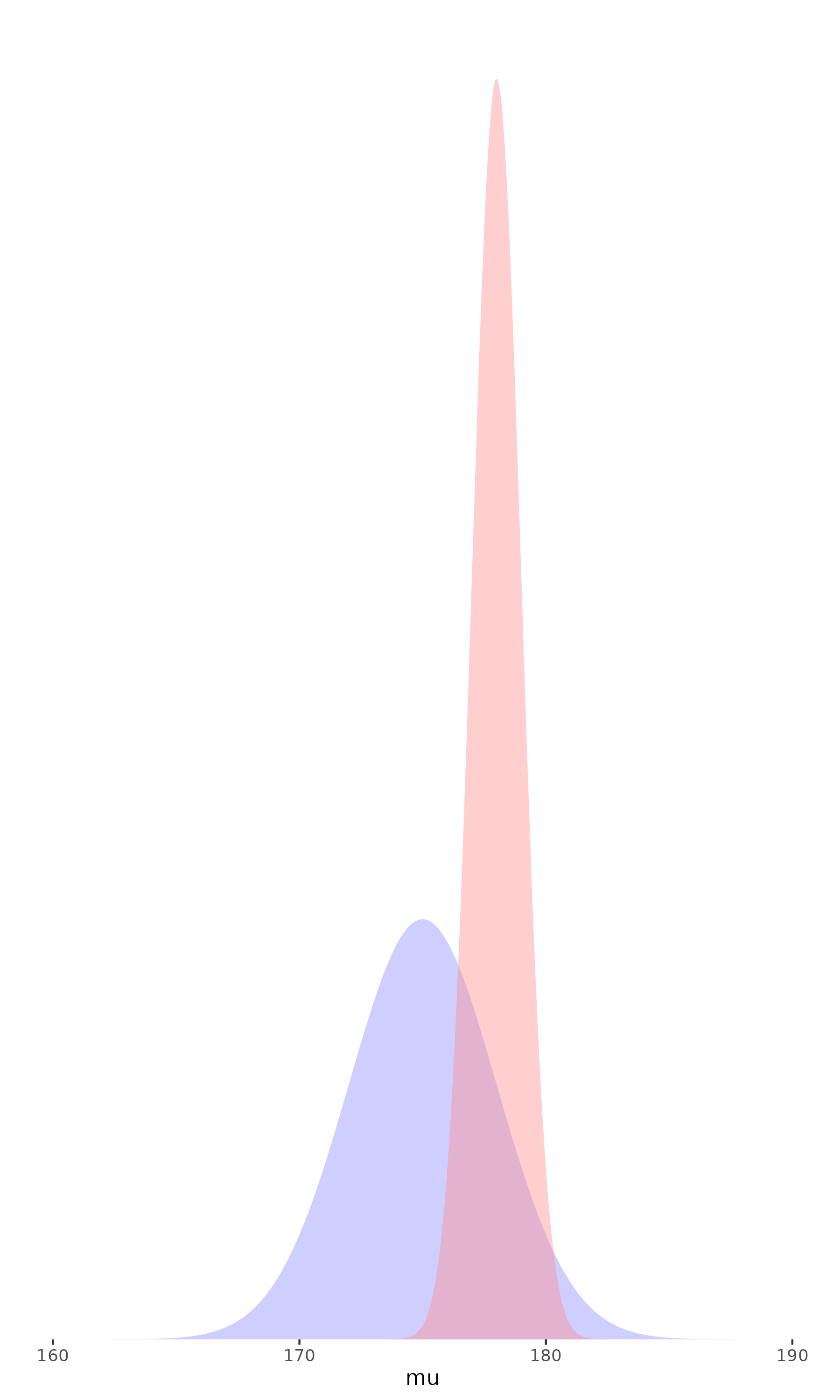
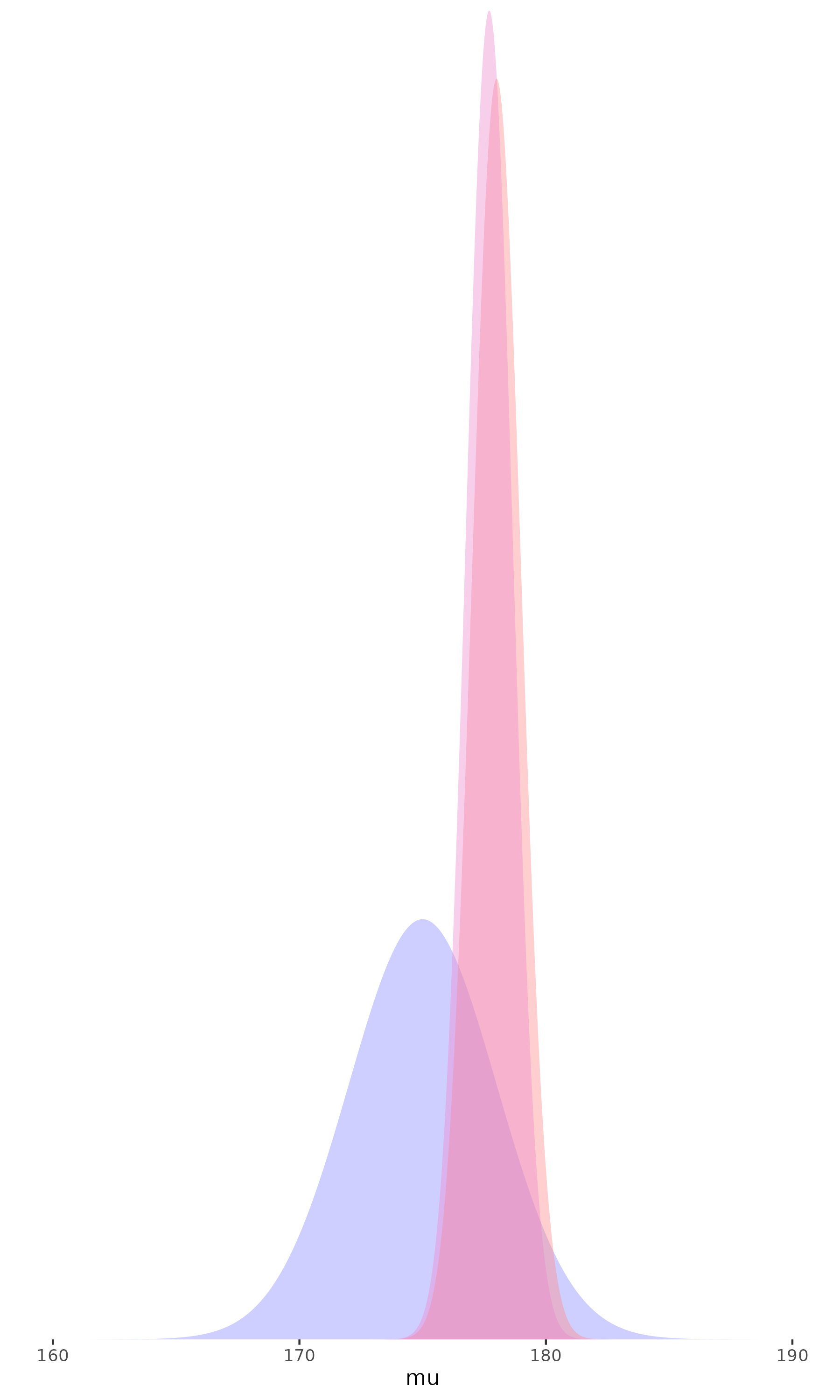
  • The more data we have,
    the less the prior matters

Why Bayesian analysis?

  • Our objective is usually to conclude something about the likely values of a treatment effect (or other outcome of interest)

  • There is usually at least some prior evidence relevant to the research question

    • Be explicit and transparent about the use of external evidence, judgements, and assumptions

  • Can be much more flexible than traditional approaches

    • Using more—and more varied—sources of data

    • More flexible models tailored to particular situations

  • Interpretation of results is much more intuitive (and relevant) than most traditional statistical methods

Presentation and interpretation

  • Bayesian analyses are often quite complex, and care is needed in presentation and interpretation

  • The prior(s) used should always be explicitly stated and justified

    • Sensitivity to different plausible priors should be considered

  • Bayesian analysis produces an estimated parameter distribution, not a single point estimate

    • The mean or median can be used as a central estimate
    • Quantiles of the distribution can be used to generate credible intervals
    • The probability of specific ranges of parameter values (e.g. \(\mathrm{Pr}(\theta > 0)\)) might be of interest

  • It is important to note (as in classical analyses) that the distribution captures uncertainty in the parameter estimate, not between-person variability in treatment effects

Comparing classical and Bayesian approaches

  • Maximum likelihood
    • Classical approaches use the likelihood (i.e. observed data) alone
    • Bayesian approaches combine the observed data likelihood with prior beliefs
  • Hypothesis testing
    • The classical p-value is not \(\mathrm{Pr}(\text{no treatment effect})\)
    • Bayesian analysis can tell us \(\mathrm{Pr}(\text{no treatment effect})\) (or any other probability statement about the parameters of interest)
  • Confidence intervals
    • Again, the classical confidence interval is not strictly a probability statement
    • In some (many) cases, classical confidence intervals are identical or very similar to Bayesian equivalents assuming no useful prior information
    • When prior information is available, Bayesian credible intervals incorporate that information

Examples

Examples


  • These examples are taken from Bayesian Approaches to Clinical Trials and Health-Care Evaluation by Spiegelhalter et al. (2003), and Bayesian Data Analysis (Third edition) by Gelman et al. (2020)


  • I hope to give some idea of the range and flexibility of Bayesian analysis


  • We will focus on the ‘What’ and the ‘Why’, not on the ‘How’

A simple RCT analysis

  • The GREAT trial was a study of a new drug for early treatment after myocardial infarction, compared with placebo

  • The primary outcome was 30-day mortality rate, with data:

New Placebo
Death 13 23 36
No death 150 125 275
163 148 311

A simple RCT analysis

  • Standard analysis of these data gives an OR of (13 / 150) / (23 / 125) = 0.47, with 95% CI 0.24 to 0.97

    • That is, a fairly large reduction in mortality, just reaching statistical significance at the 5% level
  • From a Bayesian perspective, we need to consider what our prior belief is (was) on the plausible range of true effects, and how these results should cause us to revise those beliefs

  • Prior distribution was based on the subjective judgement of a senior cardiologist, informed by previous published and unpublished studies

    • ‘an expectation of 15–20% reduction in mortality is highly plausible, while the extremes of no benefit and a 40% relative reduction are both unlikely’

    • Two initial thoughts on this prior:

      • This is a strong prior judgement, compared to the amount of information provided by the trial

      • If we are already confident that the treatment is effective, why are we doing the trial?

  • Combining this prior with the observed data gives posterior estimate of 0.73 (95% credible interval 0.58 to 0.93)

A simple RCT analysis

  • Bayesian analysis can also be used to ask how the results of this trial should change the views of a reasonably skeptical observer

    • That is, with no prior view one way or the other, but believing large treatment effects are unlikely

  • Assuming a prior centred on no effect (OR = 1), with 95% interval from 50% reduction (OR = 0.5) to 100% increase (OR = 2):

  • Posterior OR = 0.70 (95% interval 0.43 to 1.14), i.e., no effect would still be considered reasonably plausible

Multiplicity and hierarchical models

  • Problems of multiplicity are well-recognised in traditional statistical analyses
    • If we test multiple outcomes, multiple subsets of participants, multiple treatment group contrasts, we will inevitably find some ‘significant’ results, even if there are no true effects
  • In a Bayesian analysis, these multiple endpoints can often be nested within a larger hierarchical model

Educational coaching interventions in 8 schools

  • A study was performed of coaching programs to improve SAT scores in each of 8 schools
    • Estimates of the treatment effect were obtained separately from each school
School Estimated treatment effect Standard error of effect estimate
A 28 15
B 8 10
C −3 16
D 7 11
E −1 9
F 1 11
G 18 10
H 12 18

Educational coaching interventions in 8 schools

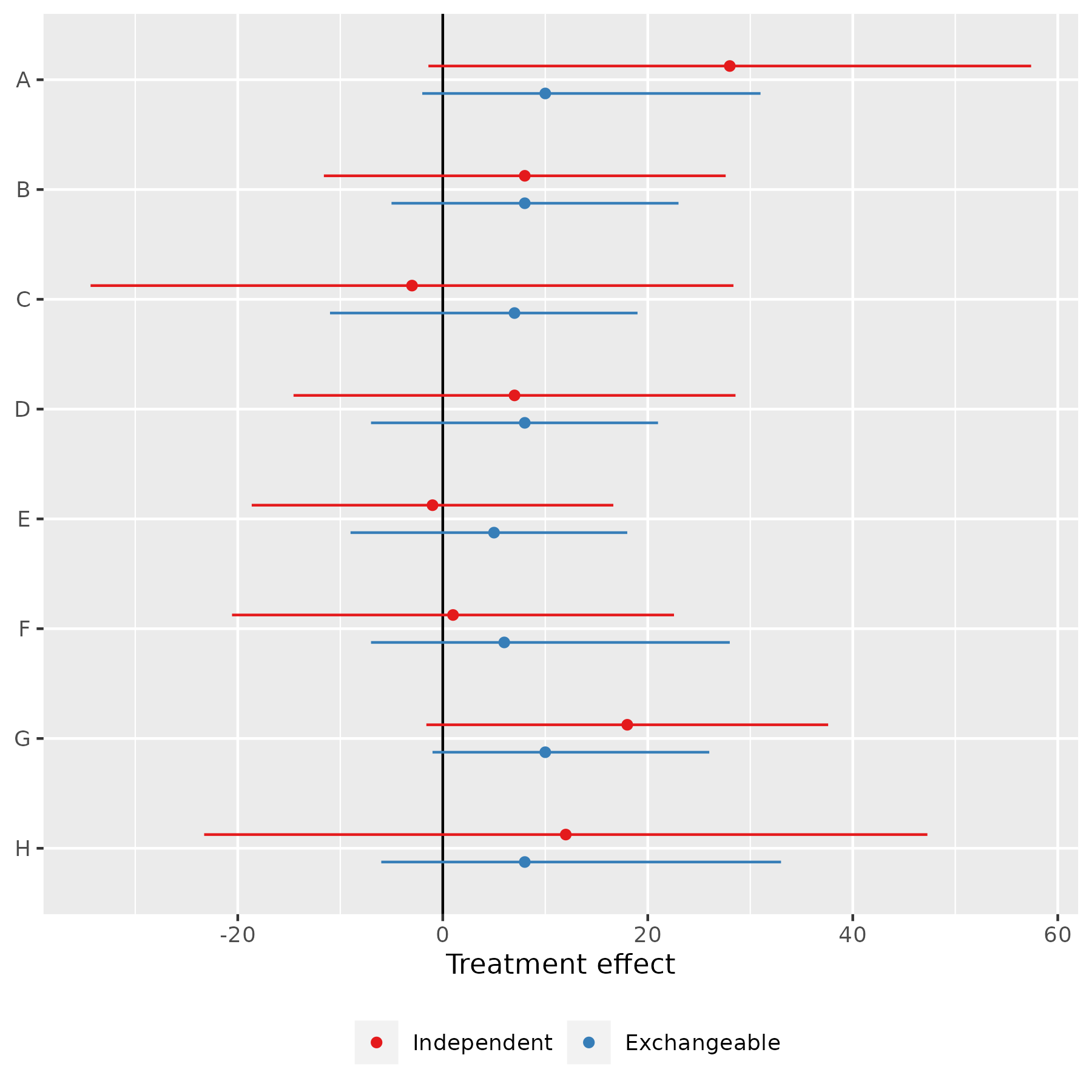
  • We can distinguish 3 different assumptions about the relationship between these estimates:

    • Identical parameters: All the true effects are identical, and the observed differences are due to sampling variation

    • Independent parameters: The true effects are independent—knowledge about one tells us nothing about the likely values of the others

    • Exchangeable parameters: The true effects are different, but drawn from a common distribution

      • The results from each school will affect our estimate of that common distribution, and therefore our estimate of the ‘true’ effect in the other schools

Educational coaching interventions in 8 schools

  • What do these different assumptions imply for our results and interpretation?

    • Identical parameters: We can pool the results from all studies (weighted by the inverse of the sampling variances)

      • We get an estimate of 7.7 points (S.E. 4.1) for the (common) treatment effect in all schools

    • Independent parameters: Take the estimates in the table at face value

    • Exchangeable parameters: Estimate a Bayesian hierarchical model

      • Assume the ‘true’ effects in each school are drawn from a normal (or other) distribution, and estimate the parameters (mean, sd) of that distribution

      • This requires us to specify prior beliefs about the mean and standard deviation of the effect distribution
        (For now, we assume non-informative prior distributions for both)

      • The effects for all schools are pulled towards the sample mean (between 5 and 10 points, instead of between –3 and 28, but with substantial uncertainty)

Meta-analysis

  • Similar hierarchical models can be used for meta-analysis as well

  • We consider an example of a meta-analysis of beta-blockers for reducing mortality after myocardial infarction

  • The study included 22 clinical trials, with data for the first few as shown

Study Control Treated Log(OR) SE
1 3/39 3/38 0.028 0.850
2 14/116 7/114 -0.741 0.483
3 11/93 5/69 -0.541 0.565
4 127/1520 102/1533 -0.246 0.138
5 27/365 28/355 0.069 0.281
6 6/52 4/59 -0.584 0.676
7 152/939 98/945 -0.512 0.139
8 48/471 60/632 -0.079 0.204

Meta-analysis

  • As before, if we assume exchangeability between the studies, we can estimate a Bayesian hierarchical model for the treatment effects

  • The results, using a non-informative prior, are

Estimand 2.5% 25% Median 75% 97.5%
Mean −0.37 −0.29 −0.25 −0.20 −0.11
Standard deviation 0.02 0.08 0.13 0.18 0.31

Meta-analysis

  • There are several estimands that may be of interest:

    • The mean of the distribution of effect sizes

    • The effect size in any of the observed studies

    • The effect size in a new comparable study

Estimand 2.5% 25% Median 75% 97.5%
Mean −0.37 −0.29 −0.25 −0.20 −0.11
Standard deviation 0.02 0.08 0.13 0.18 0.31
Predicted effect −0.58 −0.34 −0.25 −0.17 0.11

Generalised evidence synthesis

  • Observational data can often complement RCT evidence

    • (Well-conducted) RCTs have good internal validity, but possibly limited external validity

    • Observational studies are more prone to bias, but better capture real-world practice

  • There may be value in incorporating both types of evidence to better answer real-world effectiveness questions

Generalised evidence synthesis

  • From a hierarchical Bayesian perspective, there are several ways we might conceptualise the relationships between observational and experimental evidence:

    • Irrelevance: Observational studies are subject to bias and we shouldn’t include them

    • Exchangeable: Studies are exchangeable within types (e.g. observational, RCT), and mean study-type effects are exchangeable

    • Discounted: Put less weight on the observational studies to reflect their higher risk of bias

    • Functional dependence: Model the effect as a function of e.g. participant characteristics, which might differ between observational and RCT studies

    • Equal: Use all evidence from both study types without adjustment

  • There is obviously a lot of scope to specify different models here—careful sensitivity analyses are crucial

Synthesis of breast cancer screening studies

  • Five RCTs and five observational studies

  • We consider a three-level hierarchical exchangeable model:

    • As in the educational coaching example, the ‘true’ effects in each study are assumed to be different (due to e.g. different screening protocols, populations, etc.), but drawn from a common distribution

    • We observe for each study a random outcome around the true effect due to sampling variation

    • Unlike the educational coaching example, the common distribution from which each study’s true effect is drawn is not universal, but study type-specific—these study-type mean effects are themselves drawn from a higher-level distribution

  • We need to specify prior distributions for the overall population effect, the between-type variance, and the between-study variance for each type

    • As before, for now we will assume weakly informative distributions

Synthesis of breast cancer screening studies

Summary

  • Bayesian analysis helps us answer the fundamental question: What should we believe about a treatment effect (or other parameter), taking account of all available evidence?

    • Requires us to explicitly consider and specify what evidence and judgements should be included in this determination

  • Bayesian methods are particularly well-suited to (partial) pooling of evidence from different sources

    • Flexibility to design bespoke analyses tailored to specific evidence/context—requires both statistical and content-area expertise

  • Allows direct probability statements about quantities of interest, and (probabilistic) predictive statements about unobserved quantities

  • Limitations:

    • Mathematical (and computational) complexity

    • The use of perceived subjective priors is sometimes controversial

    • Flexibility perhaps raises issues of ‘data mining’ or selection of specifications to give desired results

      • Transparency and sensitivity analyses are crucial

Bayesian analysis in practice

Software

  • Historically, conducting Bayesian analysis required specialised software/modelling languages
    • BUGS (Bayesian inference Using Gibbs Sampling)
    • JAGS (Just Another Gibbs Sampler)
    • Stan
  • Most general-purpose statistical programs these days have (at least some) Bayesian methods available
    • R: e.g. rstanarm, brms
      • Also direct interface to Bayesian modelling languages with rstan, rjags
    • Stata (also StataStan)
    • SAS, SPSS ?

Model checking

  • We won’t go into this in any detail today, but it is a very important part of any Bayesian analysis
  • Posterior predictive checks
    • The model can be used to predict outcomes both in- and out-of-sample
    • Do these predictions make sense (face validity)? Are they consistent with observed data?
  • Model convergence
    • Bayesian models are generally estimated by simulation methods
    • Has the simulation converged to a stable distibution of parameter values?

References

  • Recommended textbooks:
    • Introductory: Doing Bayesian Data Analysis: A tutorial with R, JAGS, and Stan, 2nd Edition. John K. Kruschke (2015)
      • Mostly non-technical presentation of applied Bayesian analysis
      • eBook available for download via the library
    • Intermediate: Statistical Rethinking: A Bayesian Course with Examples in R and Stan, 2nd Edition. Richard McElreath (2020)
    • Intermediate: Bayesian Approaches to Clinical Trials and Health-Care Evaluation. David J. Spiegelhalter, Keith R. Abrams, Jonathan P. Myles (2004)
      • Focus on RCTs and some other clinical research designs, presenting several interesting examples of different uses of Bayesian methods
      • eBook available for download via the library
    • Advanced: Bayesian Data Analysis, 3rd Edition. Andrew Gelman, John B. Carlin, Hal S. Stearn, David B. Dunson, Aki Vehtari, and Donald B. Rubin (2013)

Return to CMOR Lunch’n’Learn presentations