Introduction to Meta-Analysis

CMOR Lunch’n’Learn

6 July 2023

Ross Wilson

Systematic reviews and meta-analyses


From Cochrane:

  • A systematic review is a study that
    “attempts to identify, appraise, and synthesize all the empirical evidence that meets pre-specified eligibility criteria to answer a specific research question”

  • Meta-analysis is the statistical combination of results from two or more separate studies

    • Meta-analysis is often one part of a systematic review

(Potential) advantages of meta-analyses


  • Improved precision
  • Evidence on generalisability
  • Resolve conflicting results from previous studies

Types of meta-analysis


  • Pairwise comparisons (i.e., intervention vs. comparator; ‘standard’ meta-analysis)
  • Network meta-analysis (comparing more than two interventions in a single model)
  • Individual participant data meta-analysis

Before doing a meta-analysis


  • Do your systematic review well:

    • Define the review aims & scope (PICO)

    • Ensure your search strategy, screening, etc. is effective

    • Identify & summarise study characteristics

    • Decide whether studies are ‘similar enough’ to be grouped & synthesized

General approach to meta-analysis


  1. Extract (or calculate) a summary statistic for each study

  2. Calculate (weighted) average effect across all studies

  3. Calculate the standard error of the summary effect (to derive confidence intervals and/or p-values)

  4. Estimate heterogeneity between studies

  5. Summarise findings graphically (usually with a forest plot)

1. Extract/calculate statistics for each study


  • For dichotomous outcomes:
    • Odds ratio
    • Risk ratio
    • Risk difference
  • For continuous outcomes:
    • Mean difference
      • (post-intervention, change from baseline, adjusted post-intervention)
    • Standardised mean difference

1. Extract/calculate statistics for each study


  • For ordinal outcomes:
    • Usually either treated as dichotomous or continuous
    • Also possible to estimate a proportional odds ratio
  • For count outcomes:
    • Again, usually treated as dichotomous or continuous
    • Rate ratio or rate difference
  • For time-to-event outcomes:
    • Hazard ratio

2. Calculate weighted effect

  • Generally, meta-analyses use an inverse-variance weighted method

\[\text{Weighted average} = \frac{\sum{Y_i W_i}}{\sum{W_i}}\]

   where \(W_i = (1 / SE_i)^2\)

  • For ratio measures, both the effects and standard errors are on the log scale
    • These can be transformed back to the original scale for reporting
  • There are slight variants to this general approach for some methods (particularly for dichotomous outcomes)

3. Calculate standard errors


  • In the general inverse-variance method, the standard error of the weighted summary statistic is

\[\text{Standard error} = \frac{1}{\sqrt{\sum{W_i}}}\]

  • Again, different formulae for some specific methods

4. Estimate heterogeneity

  • Heterogeneity is measured by

    \(Q = \sum{W_i (Y_i - \overline{Y})^2}\)

    and

    \(I^2 = \text{max}\left\{\frac{Q - (k - 1)}{Q}, 0\right\}\)

  • Q is a test statistic following a chi-squared distribution, and I2 is interpreted as the proportion of total variance in study estimates due to heterogeneity rather than sampling error

    • NOTE: I2 can be very uncertain (imprecise) when the number of studies is small

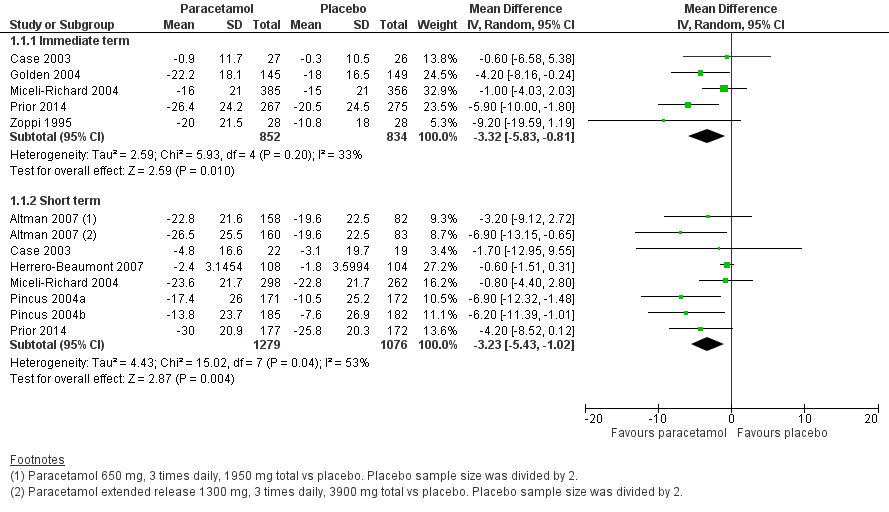
5. Summarise findings graphically


  • Meta-analyses are usually illustrated using a forest plot

  • A forest plot displays effect estimates for both individual studies and the overall meta-analysis result

  • Each study is represented by a square (usually) at the point estimate, and horizontal lines extending to bounds of the confidence interval

    • The size of the block indicates the weight assigned to that study in the meta-analysis (roughly proportional to sample size)

  • The summary result is presented as a diamond at the bottom, centred on the meta-analysis point estimate and with width showing the confidence interval

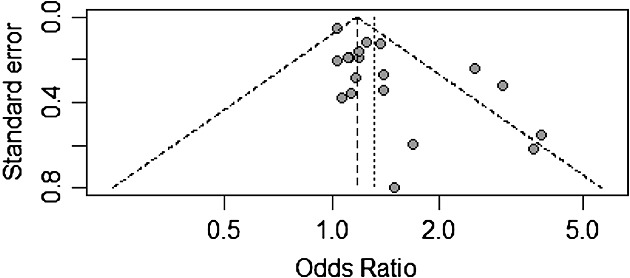
Assessing small-study bias and publication bias


  • Small sample bias: small studies may show larger intervention effects than larger studies
    • Non-reporting/non-publication bias
    • Poor methodological quality
    • Mechanistic vs. pragmatic designs
  • A ‘funnel plot’ can help detect this

Software

  • Cochrane RevMan
    • Manages all stages of the systematic review process, from design to data extraction, analysis, and visualiation
    • Free for those doing Cochrane reviews, subscription for everyone else
  • R: there are several packages for meta-analysis
    • See the Meta-Analysis Task View:
      https://cran.r-project.org/view=MetaAnalysis
    • metafor is a comprehensive package with functions for converting published results to common summary statistics, fitting inverse-variance weighted and related models, forest and funnel plots, heterogeneity measures, and diagnostic statistics (among others)

References

Return to CMOR Lunch’n’Learn presentations